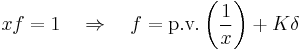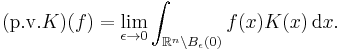Cauchy principal value
In mathematics, the Cauchy principal value, named after Augustin Louis Cauchy, is a method for assigning values to certain improper integrals which would otherwise be undefined.
Contents |
Formulation
Depending on the type of singularity in the integrand f, the Cauchy principal value is defined as one of the following:
- the finite number
- where b is a point at which the behavior of the function f is such that
- for any a < b and
- for any c > b (one sign is "+" and the other is "−"; see plus or minus for precise usage of notations ±, ∓).
- or
- the finite number
- where
- and
- (again, see plus or minus for precise usage of notation ±, ∓).
- In some cases it is necessary to deal simultaneously with singularities both at a finite number b and at infinity. This is usually done by a limit of the form
- or
- in terms of contour integrals of a complex-valued function f(z); z = x + iy, with a pole on the contour. The pole is enclosed with a circle of radius ε and the portion of the path outside this circle is denoted L(ε). Provided the function f(z) is integrable over L(ε) no matter how small ε becomes, then the Cauchy principal value is the limit:[1]
- where two of the common notations for the Cauchy principal value appear on the left of this equation.
In the case of Lebesgue-integrable functions, that is, functions which are integrable in absolute value, these definitions coincide with the standard definition of the integral.
Principal value integrals play a central role in the discussion of Hilbert transforms [2]
Examples
Consider the difference in values of two limits:
The former is the Cauchy principal value of the otherwise ill-defined expression
Similarly, we have
but
The former is the principal value of the otherwise ill-defined expression
Distribution theory
Let 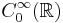 be the set of smooth functions with compact support on the real line
be the set of smooth functions with compact support on the real line 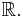 Then, the map
Then, the map
defined via the Cauchy principal value as
is a distribution. The map itself may sometimes be called the principal value (hence the notation p.v.). This distribution appears for example in the Fourier transform of the Heaviside step function.
The principal value is not exclusively defined on smooth functions ; it is enough that u be integrable, with compact support and differentiable at point 0.
It is the inverse distribution of function x and is almost the only distribution with this property :
where K is a constant and δ the Dirac distribution.
More generally, the principal value can be defined for a wide class of singular integral kernels on the Euclidean space Rn. If K(x) has an isolated singularity at the origin, but is an otherwise "nice" function, then the principal value distribution is defined on compactly supported smooth functions by
Such a limit may not be well defined or, being well-defined, it may not necessarily define a distribution. It is, however, well-defined if K is a continuous homogeneous function of degree −n whose integral over any sphere centered at the origin vanishes. This is the case, for instance, with the Riesz transforms.
Nomenclature
The Cauchy principal value of a function  can take on several nomenclatures, varying for different authors. Among these are:
can take on several nomenclatures, varying for different authors. Among these are:
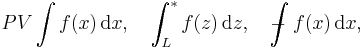
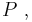 P.V.
P.V. 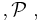
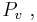
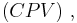 and V.P.
and V.P.
See also
References and notes
- ^ Ram P. Kanwal (1996). Linear Integral Equations: theory and technique (2nd Edition ed.). Boston: Birkhäuser. p. 191. ISBN 0817639403. http://books.google.com/books?id=-bV9Qn8NpCYC&pg=PA194&lpg=PA194&dq=+%22Poincar%C3%A9-Bertrand+transformation%22#PPA191,M1.
- ^ Frederick W. King (2009). Hilbert Transforms. Cambridge: Cambridge University Press. ISBN 978-0-521-88762-5.
This article incorporates material from Cauchy principal part integral on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.
![\lim_{\varepsilon\rightarrow 0%2B} \left[\int_a^{b-\varepsilon} f(x)\,\mathrm{d}x%2B\int_{b%2B\varepsilon}^c f(x)\,\mathrm{d}x\right]](/2012-wikipedia_en_all_nopic_01_2012/I/1f57a4f36dedbb7128e6e67a5e8d9967.png)
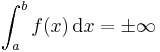
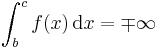
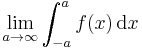
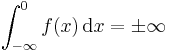
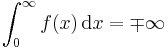
![\lim_{\varepsilon \rightarrow 0%2B} \left[\int_{b-\frac{1}{\varepsilon}}^{b-\varepsilon} f(x)\,\mathrm{d}x%2B\int_{b%2B\varepsilon}^{b%2B\frac{1}{\varepsilon}}f(x)\,\mathrm{d}x \right].](/2012-wikipedia_en_all_nopic_01_2012/I/33bdc0417410697e8c18c022eb15d73d.png)
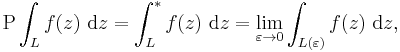
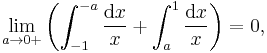
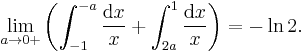
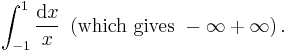
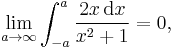
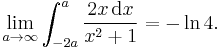
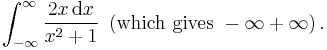
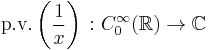
![\operatorname{p.\!v.}\left(\frac{1}{x}\right)(u)=\lim_{\varepsilon\to 0%2B} \int_{\mathbb{R}\setminus [-\varepsilon;\varepsilon]} \frac{u(x)}{x} \, \mathrm{d}x = \int_0^{%2B\infty} \frac{u(x)-u(-x)}{x}\, \mathrm{d}x \quad\text{ for }u\in C_0^\infty(\mathbb{R})](/2012-wikipedia_en_all_nopic_01_2012/I/7bd39102453c0943d193b9f85318a4dd.png)